PowerShell 7 Overview
On the 5th of April 2019, Steve Lee announced two things, the general availability of PowerShell Core 6.2 and the the next major version, PowerShell 7.
In this post we will keep track of the changes in PowerShell 7 and will provide an overview of the new lifecycle management.
Table of Contents
- Introduction
- Lifecycle
- Out-GridView makes its comeback
- Ternary Operator
- DSC
- Split Operator
- ForEach-Object Parallel
- Windows PowerShell compatibility
- Concise ErrorView
- SDDL in -Service cmdlets
- Conclusion
- Future
Introduction
This post serves as an overview of the - from our point of view - most important changes in PowerShell 7.
Lifecycle
Currently, PowerShell is under the Modern Lifecycle Policy which states that customers have to update to the latest minor version within six month in order to receive support. Patch-Versions need to be installed within 30 days.
However, PowerShell 7 will be associated with the .NET Core support Lifecycle which is Long Term Servicing (LTS).
This also supports non-LTS releases for preview releases.
You can check the .NET Core release lifecycles here.
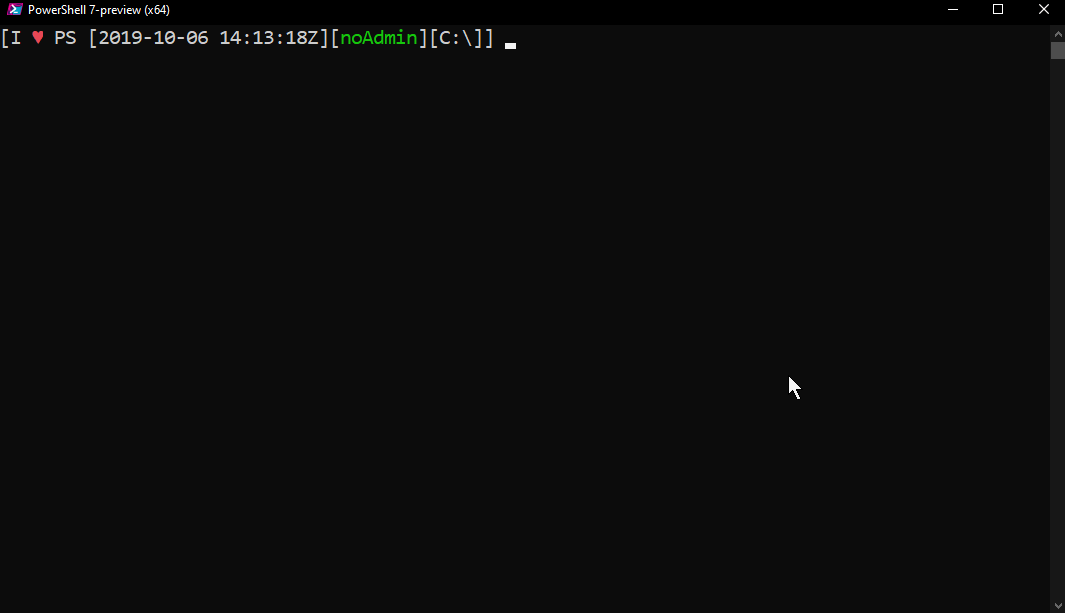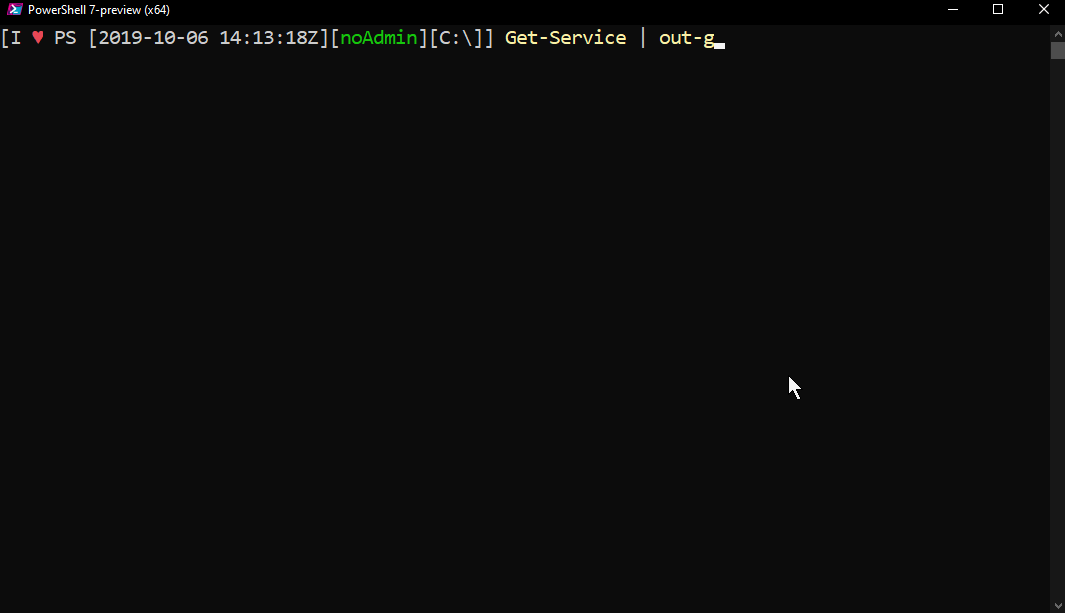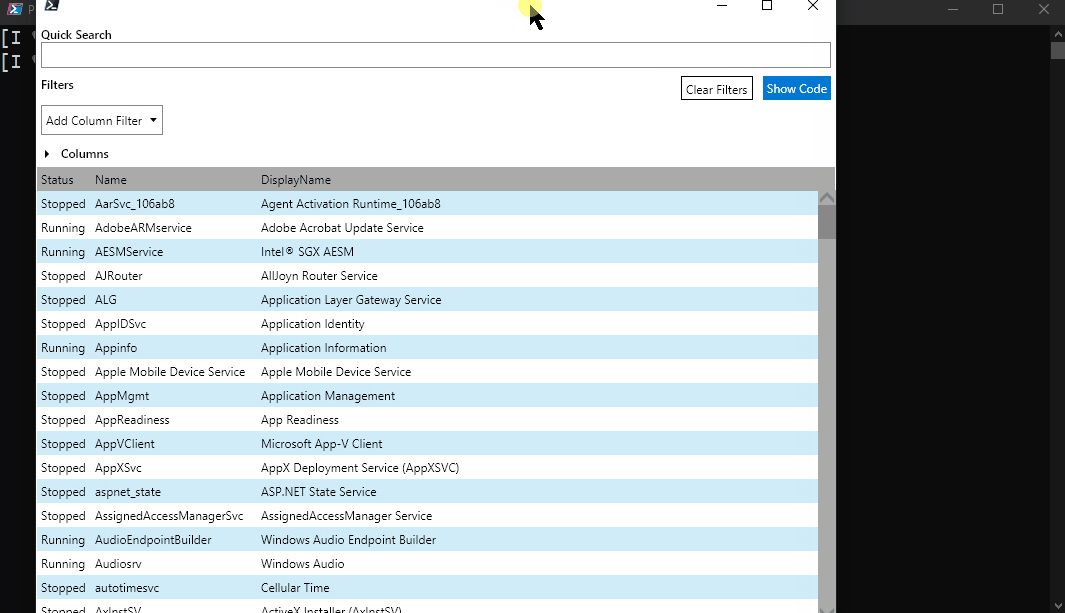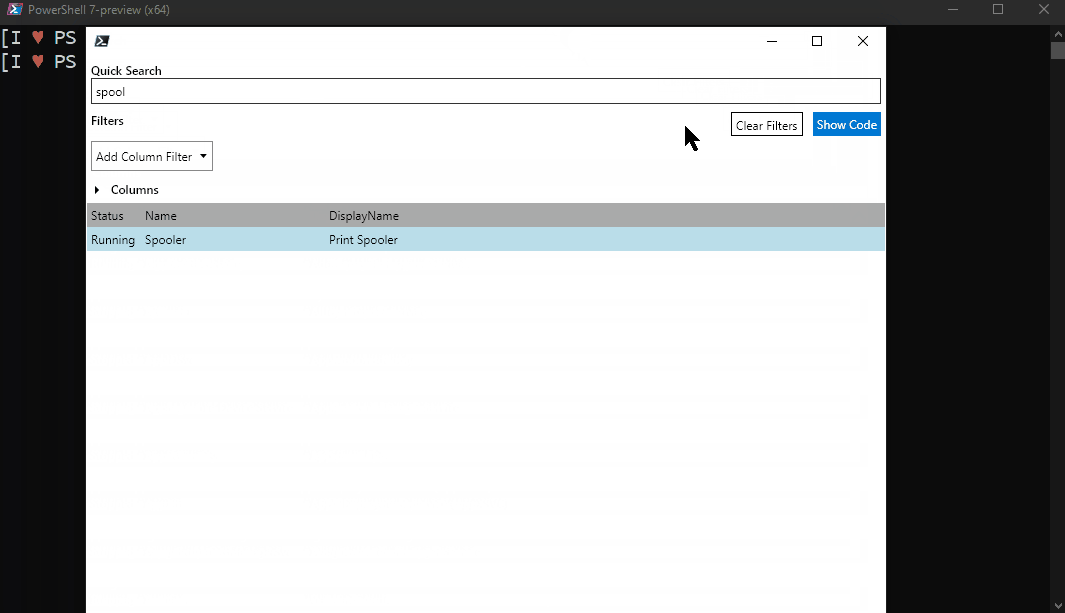
Out-GridView makes its comeback
In Windows PowerShell, Out-GridView has been around since the very beginning. It’s a simple way to quickly show the data in visualized manner with the option to filter the data, even if they are fairly limited.
To use Out-GridView in PowerShell 7, you need to install the Module ‘Microsoft.PowerShell.GraphicalTools’
1 | Install-Module Microsoft.PowerShell.GraphicalTools |
Ternary Operator
Up to this point, a ternary operator has never been natively introduced into PowerShell, until now. A ternary operator - represented by the question mark - is also known as an inline if. The condition to check is positioned to the left of the question mark, afterwards follows the statement that is executed when the condition is true. In case the condition is false, the block on the right site of the colon will be executed.
It was already possible to achieve similar behavior with PowerShell, but it’s far from a proper native implementation”
One of the old ways:
1 | @({true}, {false})[!(1 -gt 2)] |
Native implementation in PowerShell 7:
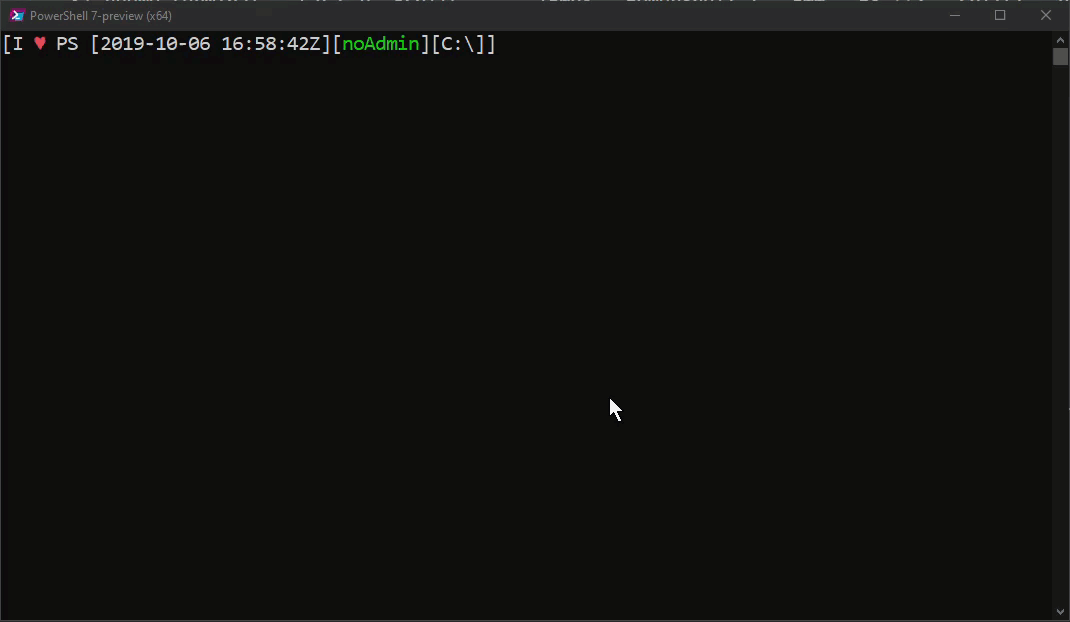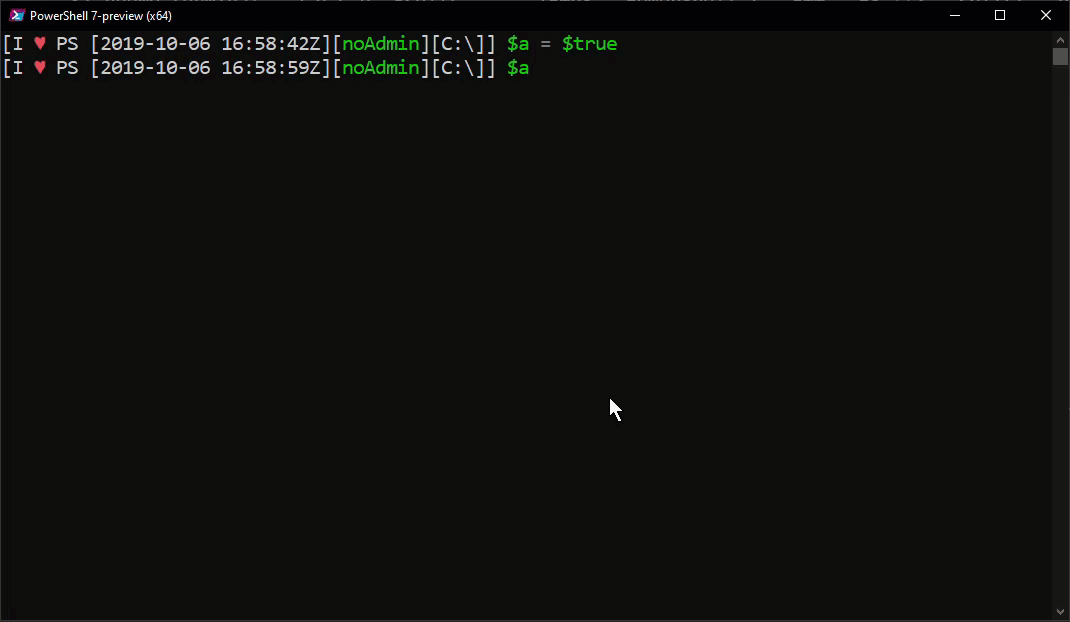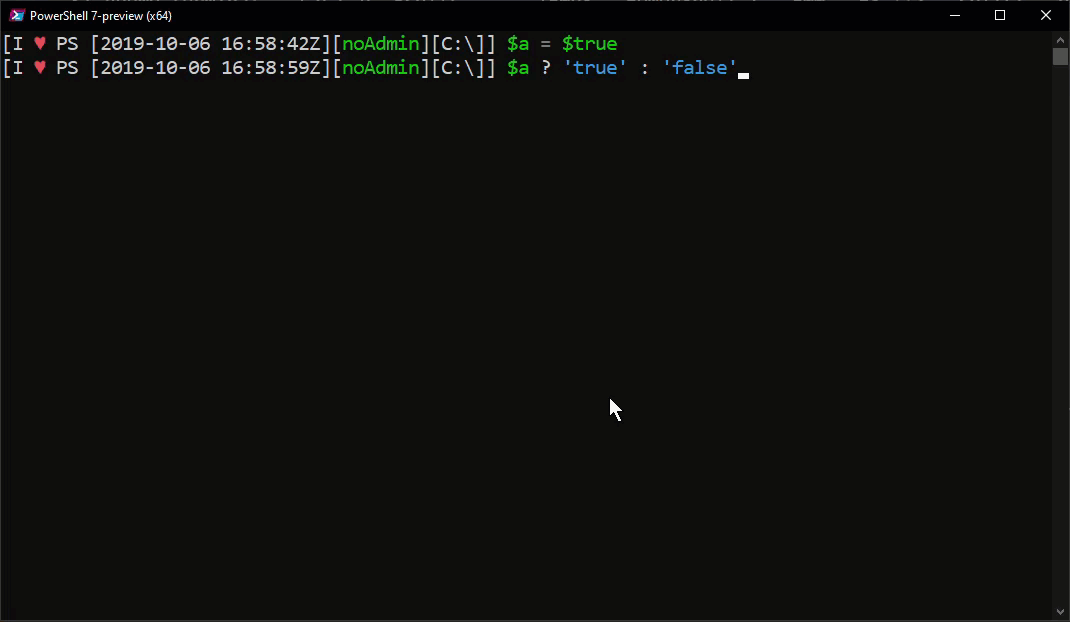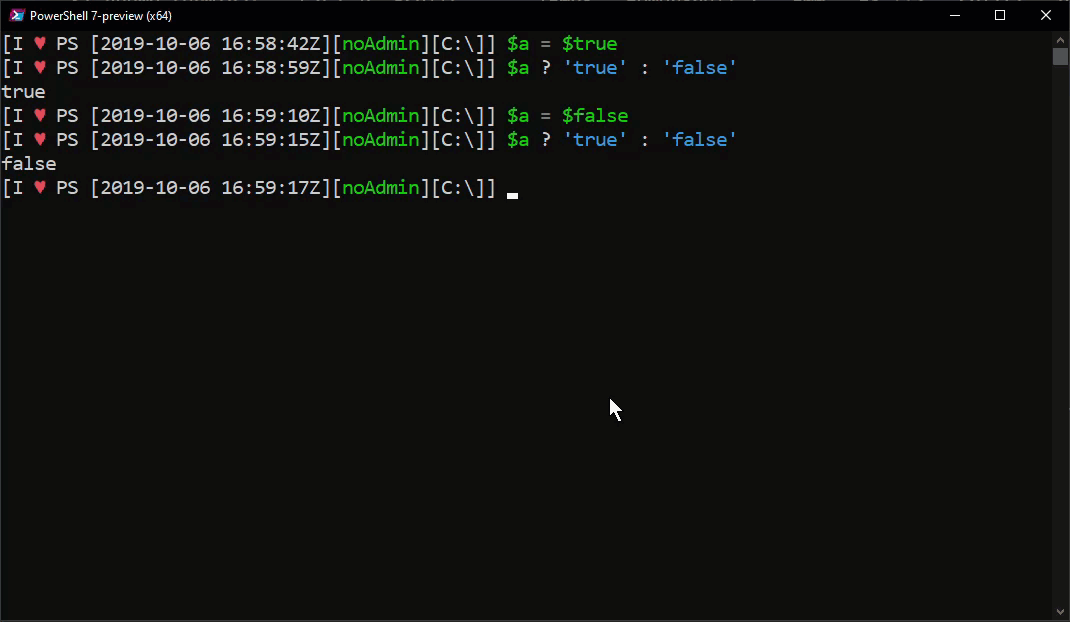
1 | $a = $true |
If $a is true, the output will be ‘true’, otherwise it will return ‘false’.
Don’t confuse it with the question mark as an alias for the Where-Object cmdlet, this still works as expected.
DSC
Invoke-DscResource
Desired State Configuration (DSC) is the declarative configuration management platform Engine written in PowerShell syntax. If you know technologies like Ansible, Chef or Puppet, this is the same concept. Normally, you would need to set up the Local Configuration Manager (LCM) on each client you want to configure with DSC, but in PowerShell 7, the new Invoke-DscResource implementation allows us to apply DSC-configurations without the LCM.
MOF Compilation
Managed Object Files (MOF) are the files that get created when a DSC-configuration is being compiled in order to be applied to a client - up to this point, this task was only possible to run on a Windows based machine, in Preview 4 of PowerShell 7, it is now also available on Linux as well as Mac OS.
Split Operator
The Split Operator splits a string into multiple strings based on the applied delimiter.
You can also set the number of how many substring you want to create:
The split operation works from left to right of the string.
PowerShell 7 introduces the Split Operator with negative number, which changes the way of the split operation, it now goes from left to right:
ForEach-Object Parallel
Do you still remember PowerShell Workflows? Introduced in PowerShell 3, it was the first time that we were able to run a ForEach-Object loops in parallel. It certainly had its drawbacks, especially the scoping was a real pain, but once it worked, it was pretty cool and - depending on the scenario - much faster than before. Also, if you ever used Workflows, you can relate to “InlineScript” madness ;)
The only application that comes to my mind, which still uses Workflows today is Azure Automation and System Center SMA.
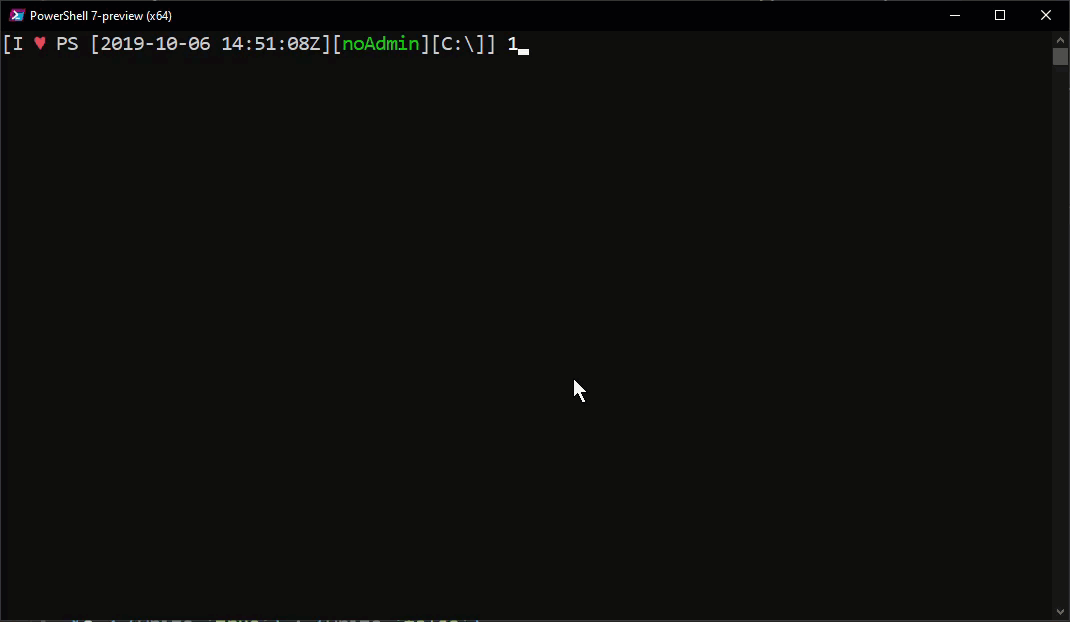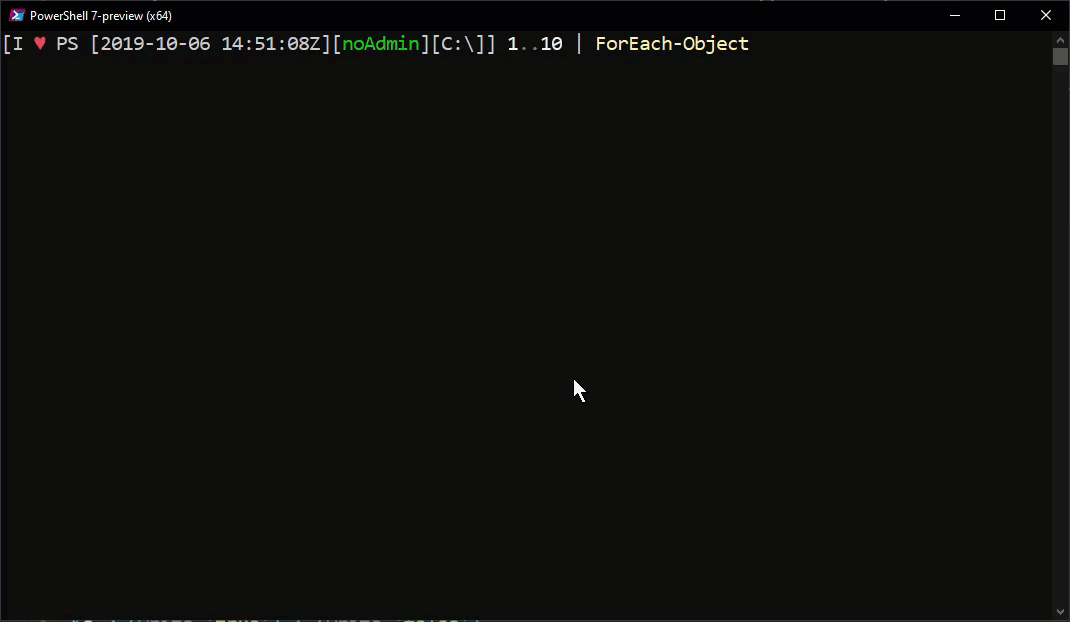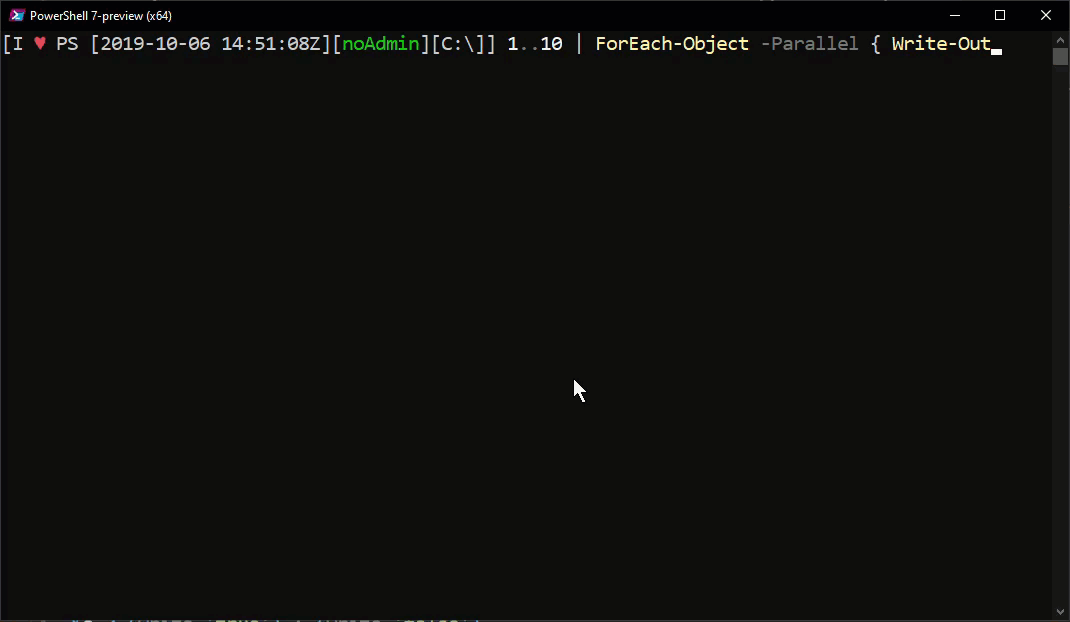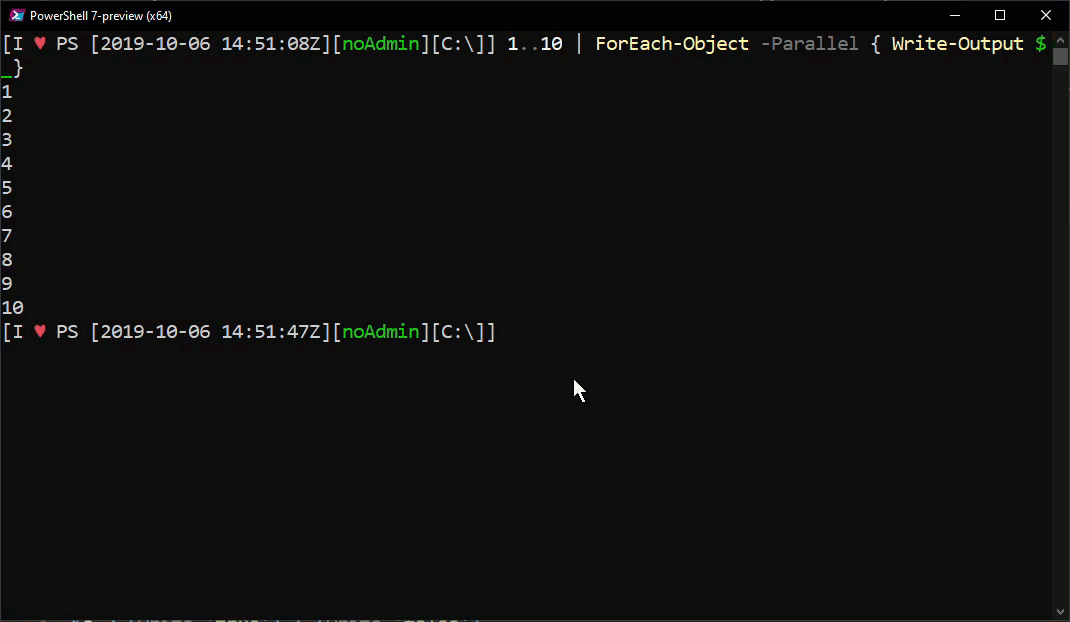
With PowerShell 7, ForEach-Object Parallel is now available without the involvement of Workflows.
1 | 1..10 | ForEach-Object -Parallel { Write-Output $_} |
The ThrottleLimit parameter indicated the number of concurrent executions - the default value is 5 but you can adjust it accordingly. However, do this carefully since there are some thing to consider.
This is only available for the ForEach-Object cmdlet, NOT the foreach keyword.
I’d suggest you read the following blog post from Paul Higinbotham to get familiar with the new feature.
Windows PowerShell compatibility
On Windows, the majority of users are still using Windows PowerShell instead of PowerShell Core - this is due to the circumstance that most modules for Windows PowerShell are not compatible with PowerShell Core yet. This is because of the current gap between .NET Core and the .NET Framework for Windows in terms of available APIs. .Net Core 3.1 will close this gap further so more PowerShell modules can be used in compatibility mode on Windows based systems.
Concise ErrorView
The Concise ErrorView has just been announced for the fifth preview by Steve Lee on October 5th.
It changes the familiar error output to a much more structured version - I’m really looking forward for this to come!
As mentioned in the tweet, the PowerShell Team would love some feedback on this - go over to the Pull Request and leave a comment.
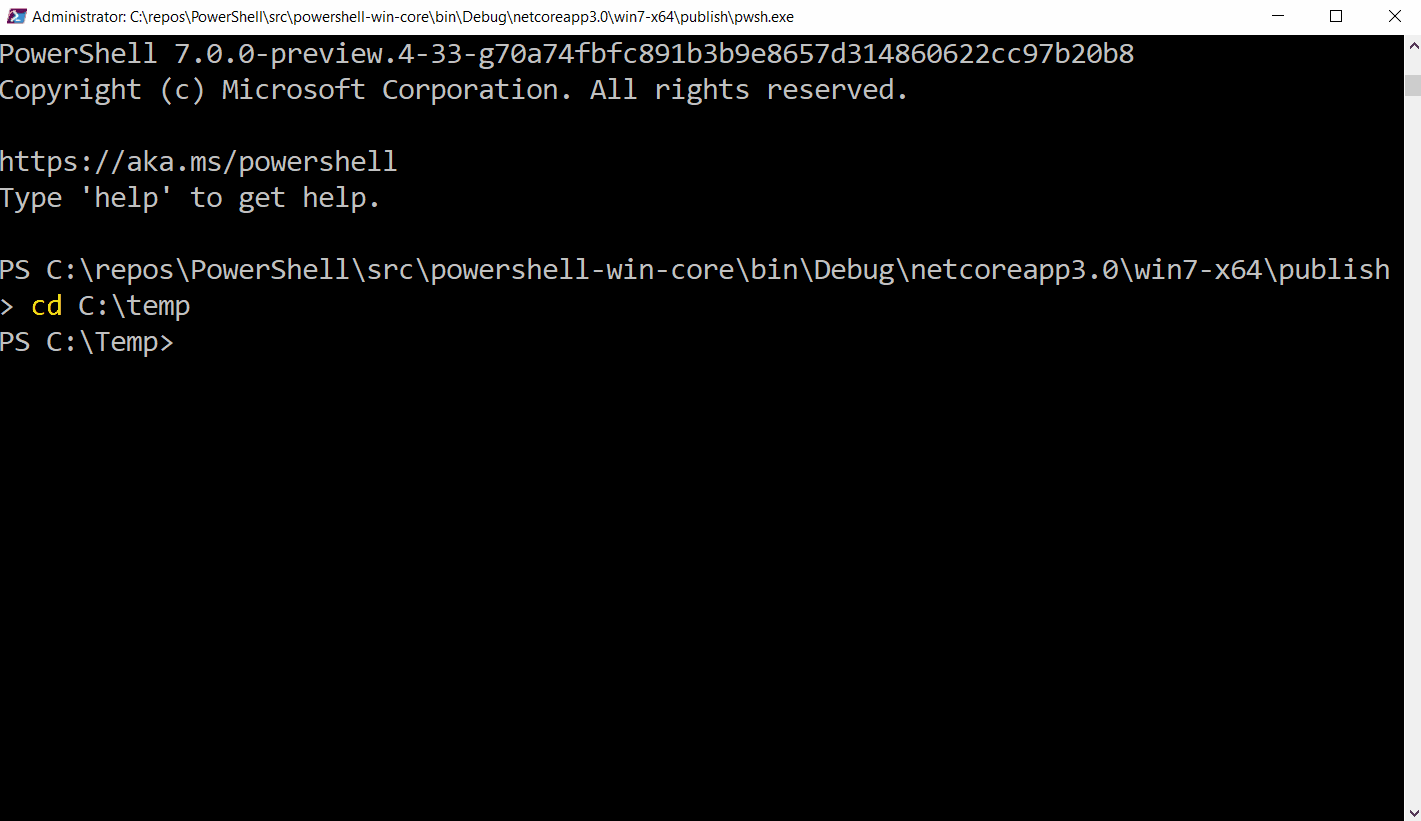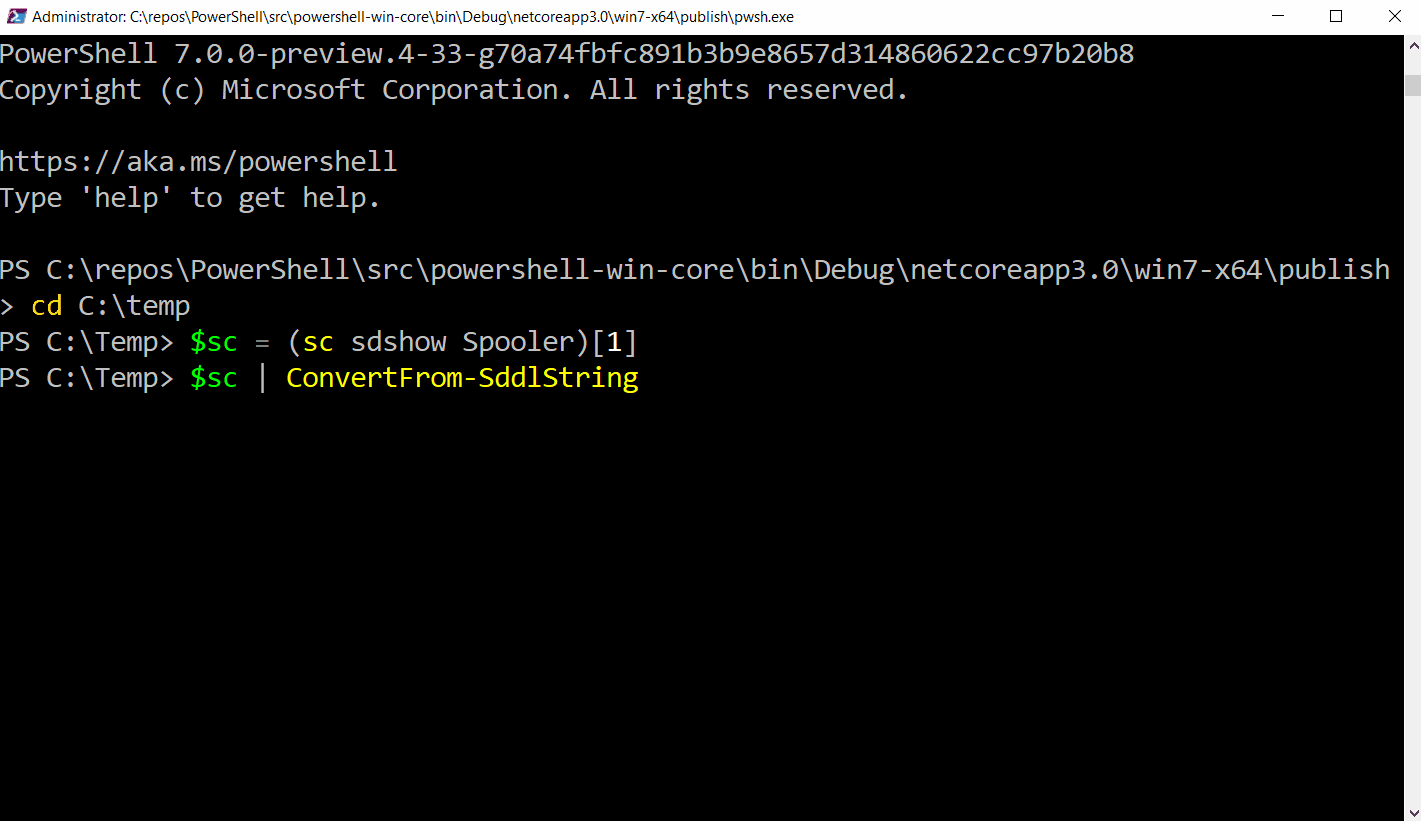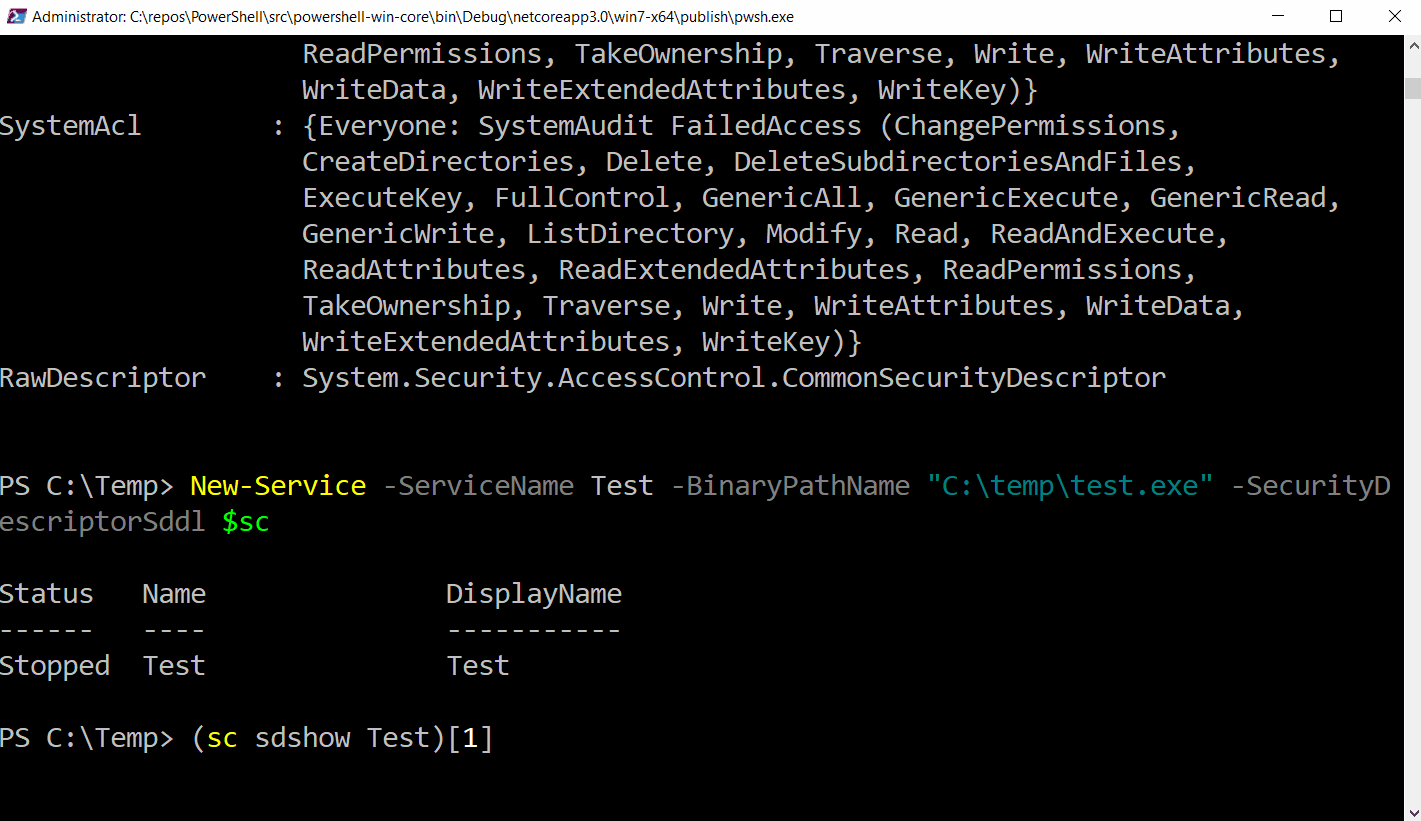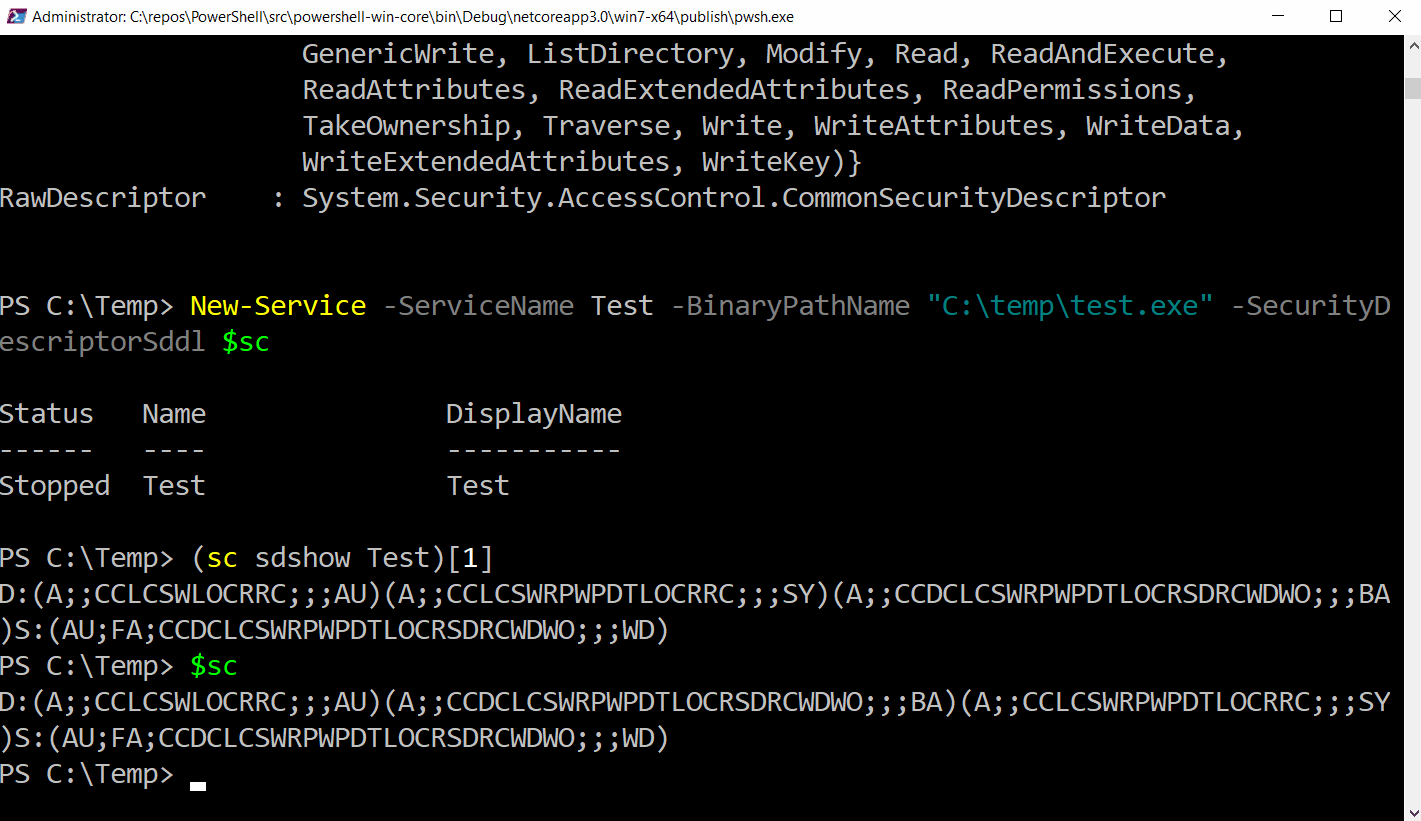
SDDL in -Service cmdlets
It’s now possible to provide a SecurityDescriptor in SDDL form with the New-Service and Set-Service functions.
Conclusion
This list is not a complete feature list, but hopefully has the most interesting ones are covered here. We will update this post, as more features are announced. If you would like to see more features covered, just leave a comment :)
Future
Since the current PowerShell 7 preview is based on .NET Core 3.0 and some new features will require .NET Core 3.1, its estimated that PowerShell 7 will be generally available when .NET Core 3.1 launches - this is scheduled for November of this year.